​一个鲜为人知的重要常数！天才般的发现：探秘欧拉常数γ！

一个鲜为人知的重要常数！天才般的发现：探秘欧拉常数γ！

我们都很熟悉两个重要常数：圆周率π和自然常数e。

然而，还有一个重要的常数——欧拉常数γ，却鲜有人知晓了。今天，我们就一起来探讨一下欧拉常数的秘密。

我们首先来思考一个问题：

1/1=1

1/1+1/2=1+1/2=1.5

1/1+1/2+1/3=1.5+1/3≈1.833

1/1+1/2+1/3+1/4≈1.833+1/4≈2.083

1/1+1/2+1/3+1/4+1/5≈2.083+1/5≈2.283

…………

那么请问：

1/1+1/2+1/3+……+1/n+……=？

我们把数列{1/n}的前n项和Σ(1/n)称之为调和级数

Σ(1/n)=1/1+1/2+1/3+……+1/n

问题转化为当n→∞时，调和级数Σ(1/n)的极限是多少？

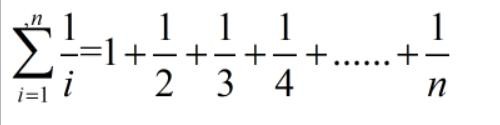
我们能够明显看到虽然调和级数是在单调递增的，但是其递增速度越来越慢。从直觉上来看，这个数列的和应该是收敛的，也就是存在一个极限值。然而事实的真相往往是反直觉的，这个数列的和恰恰是发散的，也就是趋近于正无穷大。

1/1+1/2+1/3+……+1/n+……=+∞

关于这个结论的证明有很多方法，先介绍一种最容易理解的方法：

求证：1/1+1/2+1/3+……+1/n+……=+∞

证明：1/1+1/2+1/3+……+1/n+……

=1/1+1/2+(1/3+1/4)+(1/5+1/6+1/7+1/8)+……

＞1+1/2+(1/4+1/4)+(1/8+1/8+1/8+1/8)+……

=1+1/2+1/2+1/2+……

=+∞

1/1+1/2+1/3+……+1/n+……=+∞

证毕！

接下来我们来推导一个非常重要的不等式：

我们前面学习过自然常数e，回顾一下

e=lim(1+1/n)^n，n→∞

以e为底的对数称为自然对数，记作log(e，x)=ln(x)

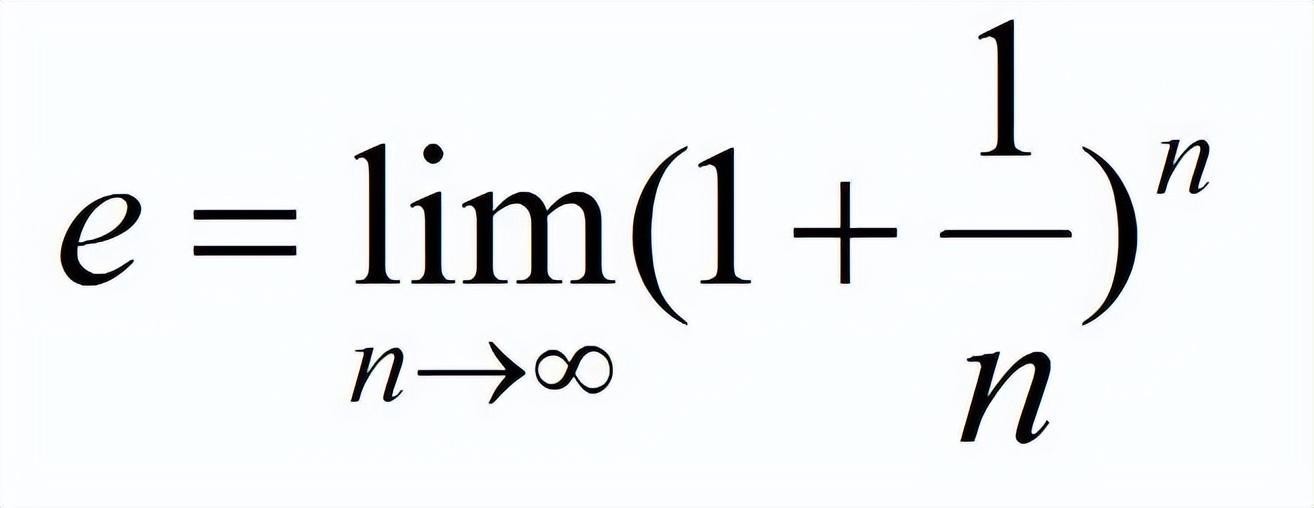
前面我们已经证明过数列{(1+1/n)^n}是单调递增的，所以

e＞(1+1/n)^n，两边同时取自然对数

e=2.71828……＞1，不等号不变向

ln(e)＞ln[(1+1/n)^n]

1＞n×ln(1+1/n)

1/n＞ln(1+1/n)

ln(1+1/n)＜1/n

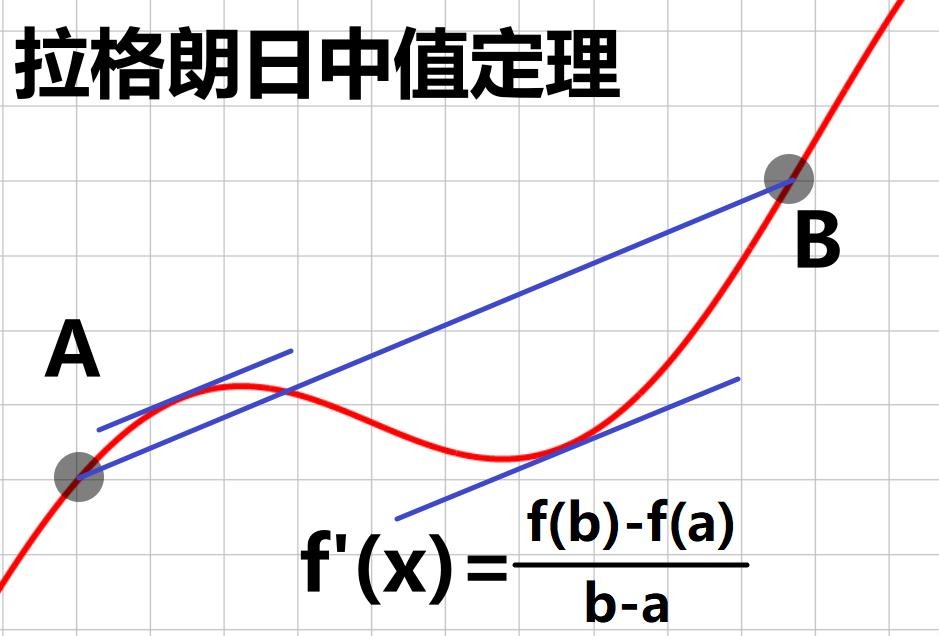
另外，利用拉格朗日中值定理，我们还可以证明

ln(1+1/n)＞1/(n+1)

1/(n+1)＜ln(1+1/n)

总结一下：

1/(n+1)＜ln(1+1/n)＜1/n

温馨提示：这个不等式非常重要！大家务必牢记！

接下来我们换一种经典方法来证明调和级数是发散的：

求证：1/1+1/2+1/3+……+1/n+……=+∞

证明：1/n＞ln(1+1/n)=ln[(n+1)/n]

1/1+1/2+1/3+……+1/n

＞ln[(1+1)/1]+ln[(2+1)/2]+ln[(3+1)/3]+……+ln[(n+1)/n]

=ln(2/1)+ln(3/2)+ln(4/3)+……+ln[(n+1)/n]

=ln{(2/1)×(3/2)×(4/3)×……×[(n+1)/n]}

=ln[(n+1)/1]

=ln(n+1)

很明显，lim[ln(n+1)]=+∞，n→∞，所以

1/1+1/2+1/3+……+1/n+……=+∞

证毕！

说了这么多，今天的主角欧拉常数γ终于要登场了。我们继续来看下面的等式：

1/1-ln1=1-0=1

(1/1+1/2)-ln2≈1.5-0.693≈0.807

(1/1+1/2+1/3)-ln3≈1.833-1.099≈0.734

(1/1+1/2+1/3+1/4)-ln4≈2.083-1.386≈0.697

(1/1+1/2+1/3+1/4+1/5)-ln5≈2.283-1.609≈0.674

…………

我们可以看到数列{Σ(1/n)-ln(n)}是在单调递减的，而且其结果都大于0。那么这个数列是否存在极限呢？

我们应该如何去证明一个数列的极限存在呢？

根据单调有界定理，如果一个数列是单调并且有界的，那么这个数列必存在极限。

接下来，我们就来分别证明数列{Σ(1/n)-ln(n)}的单调性和有界性。

Sn=Σ(1/n)=1/1+1/2+1/3+……+1/n

Tn=Sn-ln(n)=Σ(1/n)-ln(n)=(1/1+1/2+1/3+……+1/n)-ln(n)

一、有界性

前面已经证明了Sn＞ln(n+1)

Tn=Sn-ln(n)＞ln(n+1)-ln(n)=ln[(n+1)/n]=ln(1+1/n)＞ln(1)=0

Tn＞0

所以数列{Tn}={Sn-ln(n)}有下界

二、单调性

T(n+1)-Tn=[S(n+1)-ln(n+1)]-[Sn-ln(n)]

=[S(n+1)-Sn]-[ln(n+1)-ln(n)]

=1/(n+1)-ln[(n+1)/n]

=1/(n+1)-ln(1+1/n)

前面我们证明了重要不等式：

1/(n+1)＜ln(1+1/n)＜1/n

T(n+1)-Tn=1/(n+1)-ln(1+1/n)＜0

T(n+1)＜Tn

所以数列{Tn}={Sn-ln(n)}单调递减

总结一下：数列{Tn}={Sn-ln(n)}单调递减有下界

根据单调有界定理，数列{Tn}={Sn-ln(n)}必然存在极限值，我们将这个极限值叫做欧拉常数，用字母γ表示：

γ=lim[(1/1+1/2+1/3+……+1/n)-ln(n)]，n→∞

经过计算：γ=0.577215664……

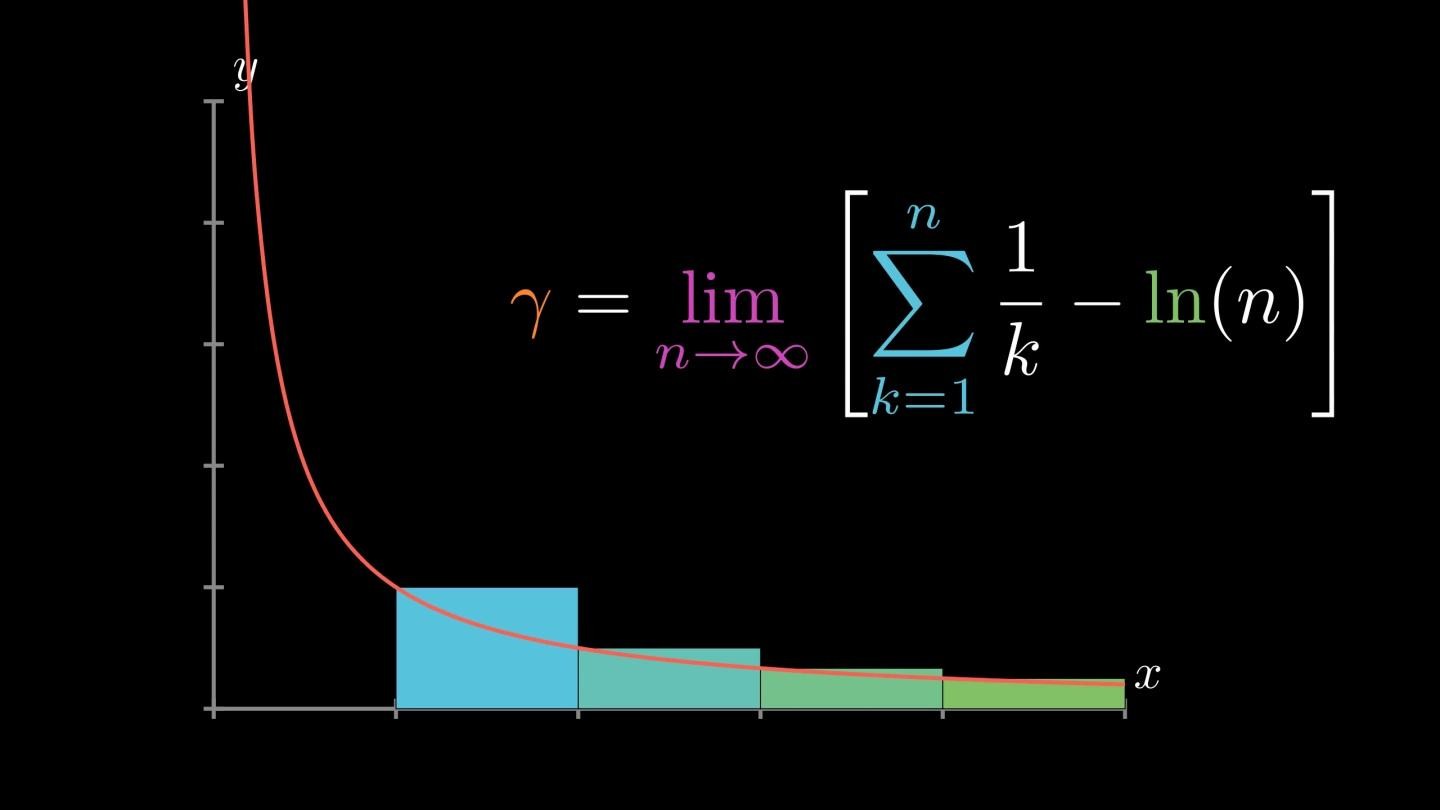
最后，还有一个非常有意思的结论：

对于级数Σ(1/n^s)，前面我们已经证明了，当s=1时，它就是调和级数Σ(1/n)，这个级数是发散的。

但是，非常神奇的是，一旦当s＞1，哪怕s=1.000……0001，级数Σ(1/n^s)都是收敛的，都存在确定的极限值。关于这一点的证明，我们后面再来讨论。